Quadrilaterals ⇒⇒ Exercise 8.1

Question 1

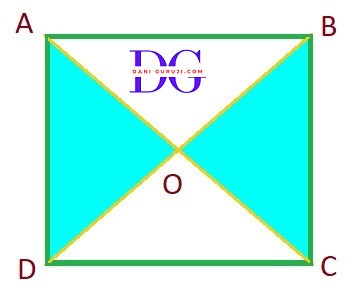
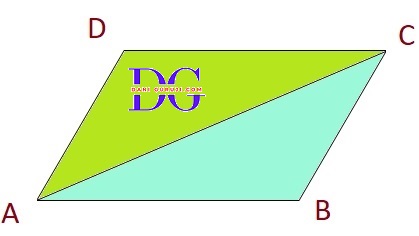
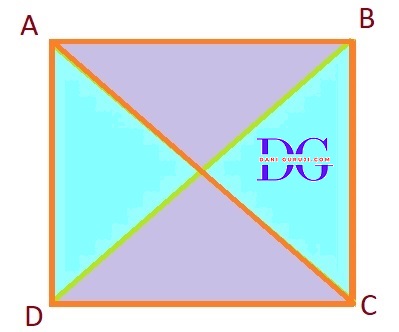
If the diagonals of a parallelogram are equal, then show that it is a rectangle.

Solution :

Let's start with a parallelogram, ABCD . It has two diagonals, AC and BD. We are given that these two diagonals are equal in length AC = BD.

And also given that,

AD = BC and AB = CD (in parallelogram opposite side are equal)

To Prove:

We've shown it's a rectangle, means it's one angle is 90° .

Consider the Δ ABC and Δ ABD:

⇒ BC = AD

( In any parallelogram, opposite sides are equal, )

⇒ AC = BD

( Given, diagonals are equal. )

AB = AB

( This is a common side for both triangles.)

∴ Δ ABC $\cong$ Δ ABD

( by the SSS congruence rule. )

Congruent triangles have equal angles

In part (i), we know that Δ ABC $\cong$ Δ ABD

This means that corresponding parts of congruent triangles are equal (CPCT).

Therefore, $\angle $ABC = $\angle $DAB.

Since $\angle $ABC , $\angle $DAB are a linear pair, their sum is 180°

$\angle $ABC + $\angle $DAB = 180°

2 $\angle $ABC = $ { 180° }$

( Since we've already shown that $\angle $ABC = $\angle $DAB.)

$\angle $ABC = $ { 180° \over 2}$

$\angle $ABC = $ { 90° }$

This shows that one of the angles of the parallelogram is a right angle.
A parallelogram with one right angle is, by definition, a rectangle.

Question 2

Show that the diagonals of a square are equal and bisect each other at right angles.

Solution :

Let's, consider ABCD to be a squre and it's diagonals AC and BD intersect each other at point O.

To Prove:

AC = BD , AO = OC and $\angle $AOB = 90° .

Consider the Δ ABC and Δ DAB:

⇒ BC = AD

( all sides of a square are equal, )

⇒ $\angle $ABC = $\angle $DAB = 90°

( all angles of a square are right angles. )

AB = AB

( This is a common side for both triangles.)

∴ Δ ABC $\cong$ Δ DAB

( by the SAS congruence rule. )

We know that Δ ABC $\cong$ Δ DAB

This means that corresponding parts of congruent triangles are equal (CPCT).

Therefore, AC = BD.

Hence, the diagonals of a square are equal in length.

Diagonals Bisect Each Other

Consider the Δ OAD and Δ OCB:

⇒ $\angle $OAD = $\angle $OCB

( Alternate angles are equal. )

⇒ BC = AD

( all sides of a square are equal, )

⇒ $\angle $ODA = $\angle $OBC

( Alternate angles are equal. )

∴ Δ OAD $\cong$ Δ OCB

( by the ASA congruence rule. )

We know that Δ OAD $\cong$ Δ OCB

This means that corresponding parts of congruent triangles are equal (CPCT).

Therefore, OA = OC and OB = OD.

Diagonals Bisect at Right Angles :

Consider the Δ AOB and Δ COB:

⇒ OA = OC

( As we had proved that diagonals bisect each other, )

⇒ BC = AB

( all sides of a square are equal, )

⇒ BO = OB

( This is a common side for both triangles. )

∴ Δ AOB $\cong$ Δ COB

( by the SSS congruence rule. )

We know that Δ AOB $\cong$ Δ COB

This means that corresponding parts of congruent triangles are equal (CPCT). Since the triangles are congruent, their corresponding angles are equal.

Therefore, $\angle $AOB = $\angle $COB.

Since $\angle $AOB , $\angle $COB form a linear pair, which means they are supplementary and add up to 180° .

$\angle $AOB + $\angle $COB = 180°

2 $\angle $AOB = $ { 180° }$

( Since we've already shown that $\angle $AOB = $\angle $COB.)

$\angle $AOB = $ { 180° \over 2}$

$\angle $AOB = $ { 90° }$

This proves that the diagonals of a square bisect each other at a right angle.

Question 3

Diagonal AC of a parallelogram ABCD bisects $\angle $A (see Fig.). Show that
(i) it bisects $\angle $C also,
(ii) ABCD is a rhombus.

Solution :

Let's start with a parallelogram, ABCD .

We're given that diagonal AC bisects $\angle $A. means

$\angle $BAC= $\angle $DAC.----------equation (1)

AD = BC and AB = CD (in parallelogram opposite side are equal and parallel )

To Prove:

AC bisects $\angle $C .

(i): AC bisects $\angle $C

When a transversal line AC intersects two parallel lines AB and DC,

⇒ $\angle $BAC = $\angle $DCA ------ equation (2)

( the alternate interior angles are equal. )

Substituting the value from equation (1)

⇒ $\angle $DAC = $\angle $DCA --------- equation (3)

Similarly, AD is parallel to BC a transversal line AC intersects them,

⇒ $\angle $DAC = $\angle $BCA ----------equation (4)

( the alternate interior angles are equal. )

By combining the results from equation 3 and 4

⇒ $\angle $DCA = $\angle $BCA.

This shows that diagonal AC divides $\angle $ C into two equal angles,
which means it bisects $\angle $C.

(ii) ABCD is a rhombus.

Consider the Δ ABC:

In part (i), we proved that

$\angle $DCA = $\angle $BCA

Also, from equation 2 in part (i), we know that

⇒ $\angle $BAC = $\angle $DCA

Combining these two, we get

⇒ $\angle $BAC = $\angle $BCA.

In any triangle, if two angles are equal, the sides opposite to those angles are also equal.

Therefore, ⇒ AB = BC

In a parallelogram, opposite sides are equal, so we know that

AD = BC and AB = CD

Since we've proven AB = BC

It follows that AB = BC = CD = DA.

A parallelogram with all four sides equal is, by definition, a rhombus.

Question 4

ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that :
(i) ABCD is a square,
(ii)diagonal BD bisects $\angle $B as well as $\angle $D.

Solution :

In rectangle ABCD, we have:

AB || CD and AD || BC.

A rectangle is a parallelogram with all angles equal to 90°.

All angles ( $\angle $A, $\angle $B, $\angle $C, $\angle $D) are 90°.

We're given that diagonal AC bisects $\angle $A , $\angle $C. means

Since AC bisects $\angle $A, we have:

$\angle $BAC = $\angle $DAC = 90°/2 = 45°

(i): ABCD is a Square

Consider the Δ ABC:

So, in ΔABC, we have:

$\angle $BAC + $\angle $B + $\angle $BCA = 180°

( The sum of angles in a triangle is 180° )

45° + 90° + $\angle $BCA = 180°

⇒ $\angle $BCA = 180° - 135°

⇒ $\angle $BCA = 45°

Since $\angle $BCA = 45° = $\angle $BAC

In any triangle, if two angles are equal, the sides opposite to those angles are also equal.

Therefore, ⇒ AB = BC

Since ABCD is a rectangle, we know that opposite sides are equal.

AD = BC and AB = CD

Since we've proven AB = BC

Combining these facts, we have: AB = BC = CD = DA.

A rectangle with all sides equal is a square. Thus, ABCD is a square.

(ii): Diagonal BD bisects $\angle $B as well as $\angle $D

Consider the square ABCD and diagonal BD.

So, in ΔABD, we have:

AB = AD

( Since all sides of a square are equal )

⇒ $\angle $ ADB = $\angle $ ABD

( the angles opposite to equal sides must also be equal. )

In a square, all angles are 90°

In ΔABD, we have:

$\angle $BAD + $\angle $ABD + $\angle $ADB = 180°

( The sum of angles in a triangle is 180° )

⇒ 90° + $\angle $ABD + $\angle $ADB = 180°

⇒ 90° + $\angle $ABD + $\angle $ABD = 180°

( Proved above, $\angle $ ADB = $\angle $ ABD )

⇒ 90° + 2$\angle $ABD = 180°

⇒ 2$\angle $ABD = 180° - 90°

⇒ 2$\angle $ABD = 90°

⇒ $\angle $ABD = 45°

$\angle $ ADB = $\angle $ ABD = 45°

This means that diagonal BD divides the 90° angle $\angle $B into two 45° angles

( $\angle $ABD = 45° and $\angle $DBC = 45° ) and the 90° angle $\angle $D into two 45° angles ($\angle $ADB = 45° and $\angle $CDB = 45° ).

Therefore, diagonal BD bisects both $\angle $B and $\angle $D.

Question 5

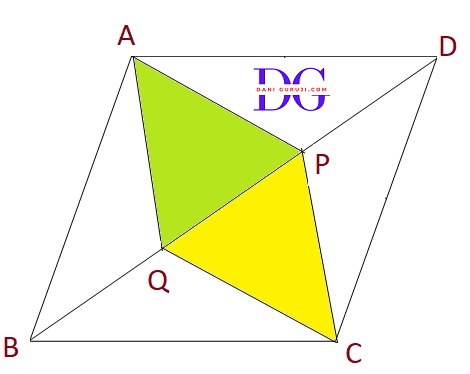
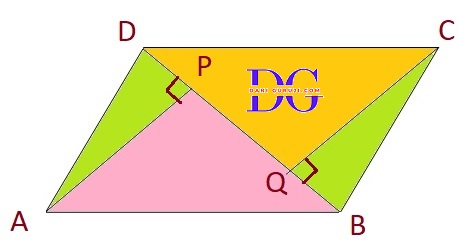
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig.) Show that:

(i) Δ APD $\cong$ Δ CQB
(ii) AP = CQ
(iii) Δ AQB $\cong$ Δ CPD
(iv) AQ = CP
(v) APCQ is a parallelogram

Solution :

(i): Δ APD $\cong$ Δ CQB

So, in Δ APD and Δ CQB we have:

AD = BC

( Opposite sides of a parallelogram are equal. )

⇒ $\angle $ ADP = $\angle $ CBQ

( These are alternate interior angles, as AD is parallel to BC (opposite sides of a parallelogram) and BD is the transversal. )

DP = BQ

( This is given in the problem statement. )

Since we have two sides and the included angle equal, we can conclude that, by Side-Angle-Side (SAS) congruence criterion :

Δ APD $\cong$ Δ CQB

(ii) Proving AP = CQ

We've just proven that Δ APD $\cong$ Δ CQB . Since the triangles are congruent, We know that, Corresponding parts of congruent triangles are equal. Therefore,

⇒ AP = CQ

(iii) Δ AQB $\cong$ Δ CPD

So, in Δ AQB and Δ CPD we have:

AB = CD

( Opposite sides of a parallelogram are equal. )

⇒ $\angle $ ABQ = $\angle $ CDP

( These are alternate interior angles, as AB is parallel to DC and BD is the transversal. )

DP = BQ

( This is given in the problem statement. )

Since we have two sides and the included angle equal, we can conclude that, by Side-Angle-Side (SAS) congruence criterion :

Δ AQB $\cong$ Δ CPD

(iv) Proving AQ = CP

We've just proven that Δ AQB $\cong$ Δ CPD . Since the triangles are congruent, We know that, Corresponding parts of congruent triangles are equal. Therefore,

⇒ AQ = CP

(v) Proving APCQ is a parallelogram

A quadrilateral is a parallelogram if its opposite sides are equal.

⇒ AQ = CP

( This is proved above in part (iv))

⇒ AP = CQ

( This is proved above in part (ii))

Since both pairs of opposite sides are equal, the quadrilateral APCQ is a parallelogram.

Question 6

ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD. Show that

(i) Δ APB $\cong$ Δ CQD
(ii) AP = CQ

Solution :

(i): Δ APB $\cong$ Δ CQD

So, in Δ APB and Δ CQD we have:

AB = CD

( The opposite sides of a parallelogram are equal in length. )

⇒ $\angle $ ABP = $\angle $CDQ

( These are alternate interior angles, as AD is parallel to BC (opposite sides of a parallelogram) and BD is the transversal. )

$\angle $APB = $\angle $CQD

( Both are right angles, as AP and CQ are perpendiculars to the diagonal BD )

Since we have two corresponding angles and a non-included side equal, we can conclude that, by Angle-Angle-Side (AAS) congruence criterion :

Δ APB $\cong$ Δ CQD

(ii) Proving AP = CQ

We've just proven that Δ APB $\cong$ Δ CQD . Since the triangles are congruent, We know that, Corresponding parts of congruent triangles are equal. Therefore,

⇒ AP = CQ

Question 7

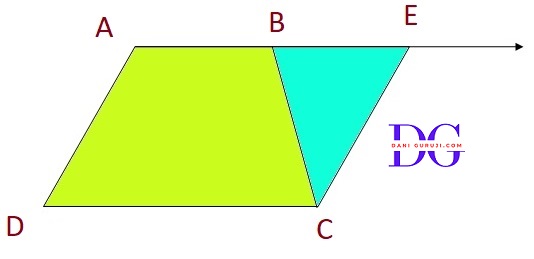
ABCD is a trapezium in which AB || CD and AD = BC. Show that:

(i) $\angle $A = $\angle $B
(ii) $\angle $C = $\angle $D
(iii) Δ ABC $\cong$ Δ BAD
(iv) diagonal AC = diagonal BD

Solution :

(i) $\angle $A = $\angle $B

We first need to do a small construction. Extend side AB and draw a line CE parallel to AD, intersecting the extended AB at point E.:

AD = CE

( Since AD || CE and AE is a transversal, ADCE is a parallelogram by construction. The opposite sides of a parallelogram are equal in length. )

⇒ AD = BC

( given )

Therefore, from above
∴ BC = CE

Consider the Δ BCE:

So, in Δ BCE, we have BC = CE, it is an isosceles triangle, which means

$\angle $CBE = $\angle $CEB ----- Equc.(1)

$\angle $ABC + $\angle $CBE = 180° ----- Equc.(2)

( Because these angles form a linear pair )

Consider, parallel lines AD and CE where AE is the transversal.

We know that consecutive interior angles are supplementary, so

$\angle $A + $\angle $AEC = 180°

$\angle $A + $\angle $CEB = 180° ----- Equc.(3)

( $\angle $AEC = $\angle $CEB, because they are the same angle )

From Equc.(2) and Equc.(3), we have

$\angle $ABC + $\angle $CBE = $\angle $A + $\angle $CEB

Since $\angle $CBE = $\angle $CEB ,

We can subtract them from both sides, which gives us

$\angle $ABC = $\angle $A

Thus, $\angle $A = $\angle $B.

(ii) $\angle $C = $\angle $D

From figure,

AB || CD

We know that the consecutive interior angles are supplementary

$\angle $A + $\angle $D = 180°

$\angle $B + $\angle $C = 180°

From part (i), we know that

$\angle $A = $\angle $B

Substituting Values of $\angle $A

$\angle $B + $\angle $D = 180°

$\angle $B + $\angle $C = 180°

By comparing these two equations, we can conclude that

$\angle $C = $\angle $D

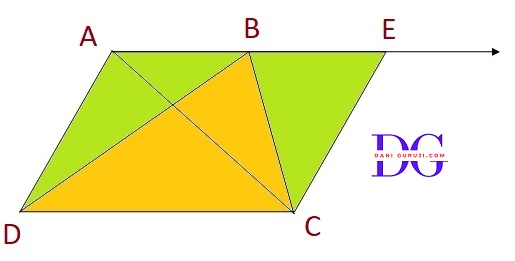
(iii) Δ ABC $\cong$ Δ BAD

So, in Δ ABC and Δ BAD we have:

AB = AB

( This is a common side to both triangles. )

⇒ $\angle $ A = $\angle $B

( Proved in part (i) )

BC = AD

( This is given )

Since two sides and the included angle are equal, we can conclude that,

ΔABC $\cong$ Δ BAD

(iv) Proving diagonal AC = diagonal BD

We've just proven that ΔABC $\cong$ Δ BAD . Since the triangles are congruent, We know that, Corresponding parts of congruent triangles are equal. Therefore,

⇒ AC = BD